https://arxiv.org/pdf/1806.01817v1.pdf
Marios Savvides
Carnegie Mellon University and Michigan State University
We have recently posted our response on the issue raised in the Reddit discussion. Please see the two links below:
New PNN Repository: https://github.com/juefeix/pnn.pytorch.update
Response on Reddit Regarding PNN Reproducibility: click here
Original PNN (PyTorch) on Github: https://github.com/juefeix/pnn.pytorch
Understanding Perturbative Neural Networks (PNN):
Convolutional neural networks are witnessing wide adoption in computer vision systems with numerous applications across a range of visual recognition tasks. Much of this progress is fueled through advances in convolutional neural network architectures and learning algorithms even as the basic premise of a convolutional layer has remained unchanged. In this paper, we seek to revisit the convolutional layer that has been the workhorse of state-of-the-art visual recognition models. We introduce a very simple, yet effective, module called a perturbation layer as an alternative to a convolutional layer. The perturbation layer does away with convolution in the traditional sense and instead computes its response as a weighted linear combination of non-linearly activated additive noise perturbed inputs. We demonstrate both analytically and empirically that this perturbation layer can be an effective replacement for a standard convolutional layer. Empirically, deep neural networks with perturbation layers, called Perturbative Neural Networks (PNNs), in lieu of convolutional layers perform comparably with standard CNNs on a range of visual datasets (MNIST, CIFAR-10, PASCAL VOC, and ImageNet) with fewer parameters.

In Local Binary Convolutional Neural Networks (LBCNN), CVPR'17, convolving with a binary filter is equivalent to addition and subtraction among neighbors within the patch. Similarly, convolving with a real-valued filter is equivalent to the linear combination of the neighbors using filter weights. Either way, the convolution is a linear function that transforms the center pixel x5 to a single pixel in the output feature map, by involving its neighbors. Can we arrive at a simpler mapping function?
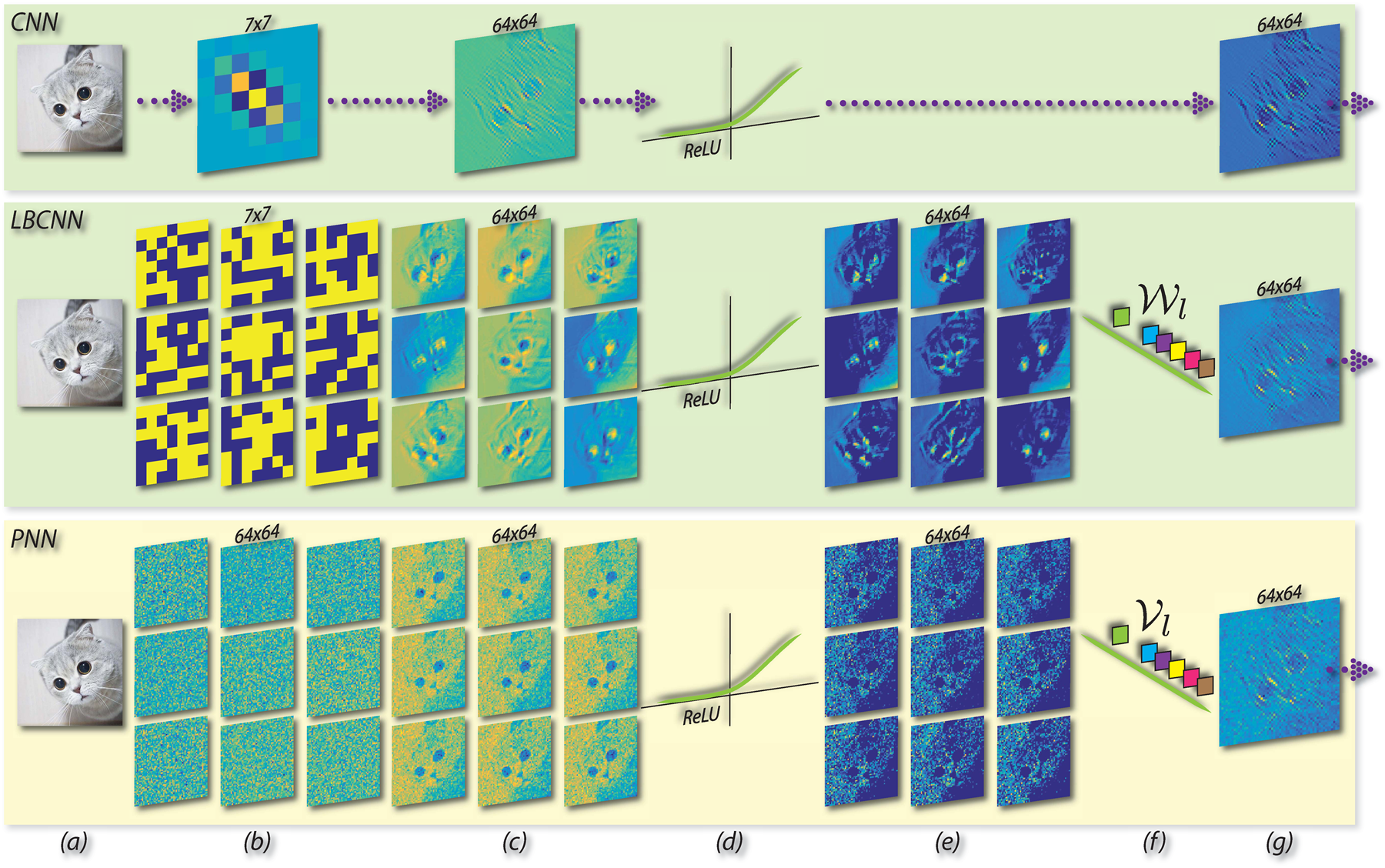
Basic modules in CNN, LBCNN, and PNN. Wl and Vl are the learnable weights for local binary convolution layer and the proposed perturbation layer respectively. For PNN: (a) input, (b) fixed non-learnable perturbation masks, (c) response maps by addition with perturbation masks, (d) ReLU, (e) activated response maps, (f) learnable linear weights for combining the activated response maps, (g) feature map.
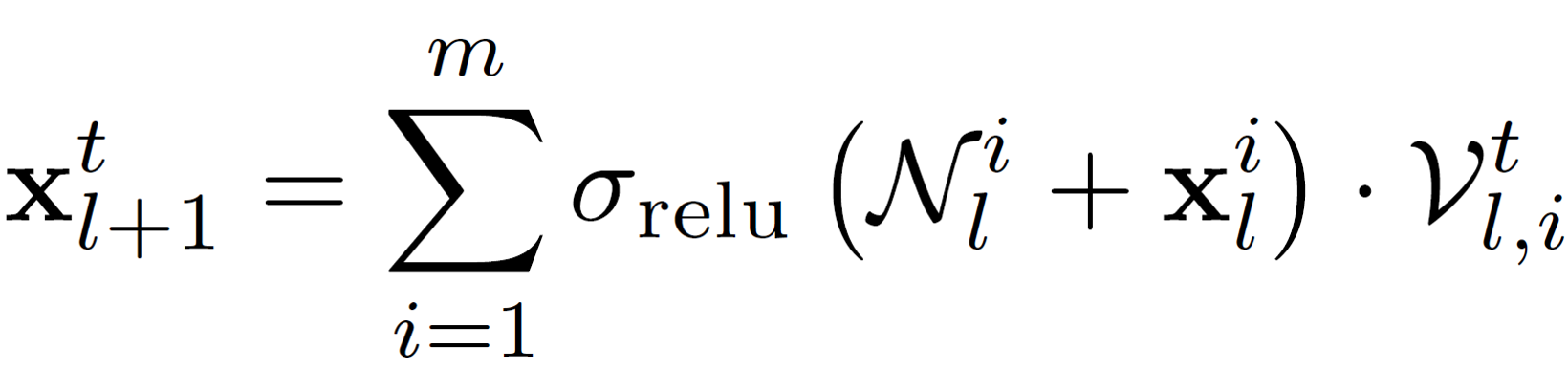
N^i is the i-th random additive perturbation mask. The linear weights V are the only learnable parameters of a perturbation layer.

Perturbation residual module.
Novel deep learning model in lieu of convolutional layers
Theoretical analysis on relating PNN and CNN
A macro view: we have shown that PNN layer can be a good approximation for any CNN layer.
A micro view: we have shown that convolution operation behaves like additive noise under mild assumptions.
On-par performance with standard CNNs (ImageNet, CIFAR-10, MNIST, and Pascal VOC)
Felix Juefei-Xu, Vishnu Naresh Boddeti, and Marios Savvides, Perturbative Neural Networks, in Proceedings of the IEEE Computer Vision and Pattern Recognition (CVPR), 2018.
@inproceedings{juefei-xu2018pnn, title={{Perturbative Neural Networks}}, author={Felix Juefei-Xu and Vishnu Naresh Boddeti and Marios Savvides}, booktitle={IEEE Computer Vision and Pattern Recognition (CVPR)}, month={June}, year={2018} }